Question:
Are Squares Rectangles? Squares: A Special Case of Rectangles Explained
Answer:
Yes, squares are rectangles
Explanation
When it comes to geometry, there are various shapes with unique properties. One such relationship is between squares and rectangles. The question often arises: “Are squares rectangles?” In this article, we will delve into the technical and mathematical aspects of squares and rectangles, understanding their defining characteristics and how they are related.
Definition of Rectangles:
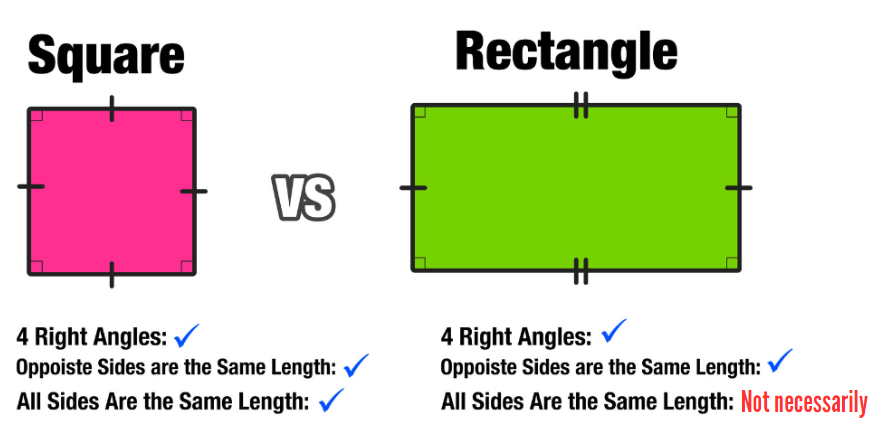
To begin, let’s define what constitutes a rectangle mathematically. A rectangle is a quadrilateral (a four-sided polygon) with four right angles, meaning all its interior angles measure 90 degrees. Additionally, opposite sides of a rectangle are parallel and equal in length. This definition forms the foundation of rectangles and their properties.

Characteristics of Squares:
Now, let’s explore squares and their unique attributes. A square is a specific type of quadrilateral that also falls under the category of rectangles. It possesses all the properties of a rectangle but with an additional constraint: all four sides of a square are of equal length. Moreover, since all angles of a square are right angles, it inherently satisfies the definition of a rectangle.
The mathematical relationship between squares and rectangles can be summarized as follows:
Every square is a rectangle, but not every rectangle is a square.
In other words, squares are a subset of rectangles, and they share the fundamental characteristics of rectangles while having an additional condition that sets them apart.
Proof:
To prove that squares are indeed rectangles, we can use the definition of a rectangle. Let ABCD be a square with sides of length ‘a.’ Since all sides of a square are equal, AB = BC = CD = DA = a. Now, let’s consider two opposite sides of the square, AB and BC. Since all angles of a square are right angles, the opposite sides are parallel. Hence, the four sides of the square are equal in length and form right angles, meeting the criteria of a rectangle.
Conclusion:
In conclusion, squares are indeed rectangles, meeting all the defining characteristics of a rectangle while having the additional property of all sides being of equal length. Understanding this mathematical relationship is crucial for a solid grasp of geometry and its various shapes. So, the next time you encounter the question, “Are squares rectangles?” you can confidently explain the technical and mathematical basis behind this relationship.
By educating ourselves about such geometric concepts, we can foster a deeper appreciation for the beauty and elegance of mathematics in our everyday lives.