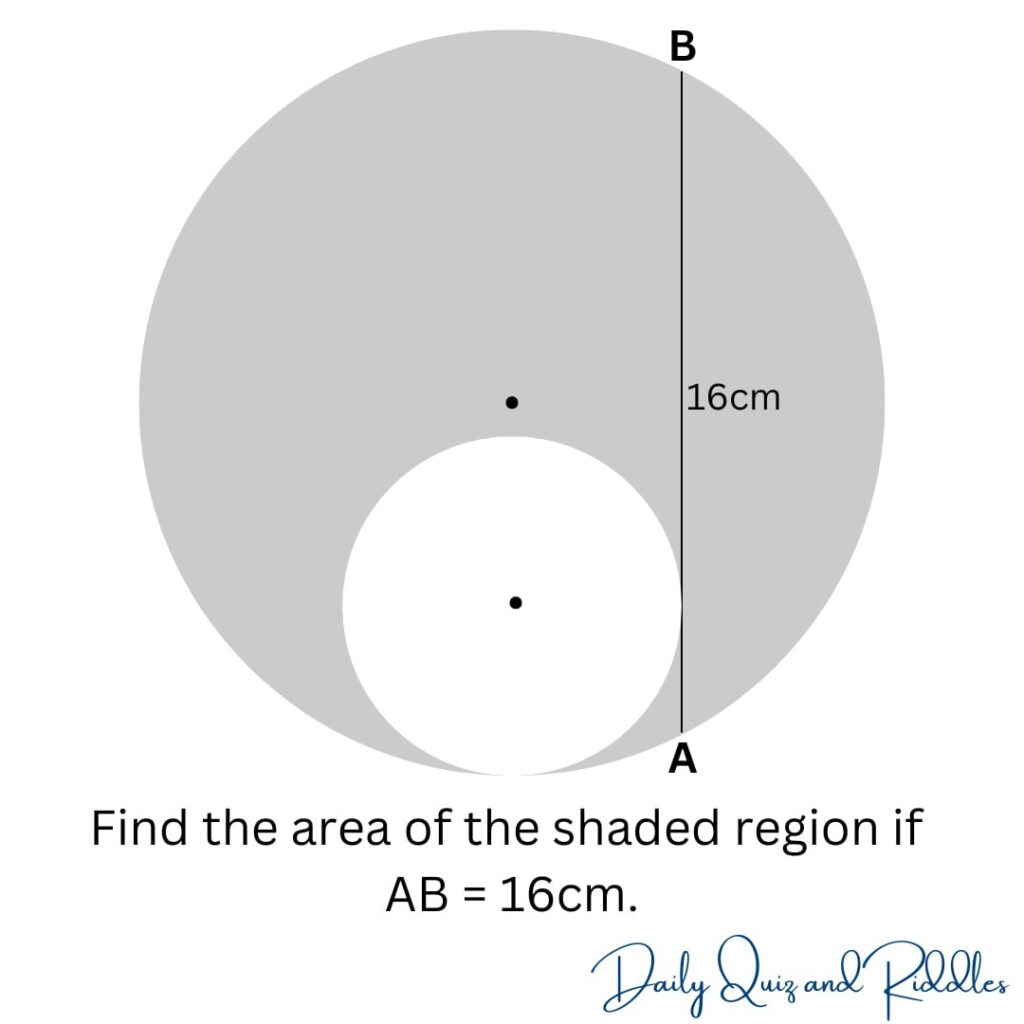
Question:
Find the area of the shaded region if AB is 16cm.
Answer:
The area of the shaded region is 201.1 square centimeters.
Explanation
Welcome to a math quiz that will challenge your geometric prowess! In this intriguing puzzle, a large circle holds a smaller circle within its bounds, creating a shaded area of mystery. Let’s embark on a journey of deductions and calculations to unlock the solution to this captivating challenge.
Step by Step: To tackle this problem effectively, we’ll introduce some crucial variables:
- Let the distance from the center of the big circle to point B be R.
- Let the distance from the point C to D be r, making BC = R, and CD = EF = r.
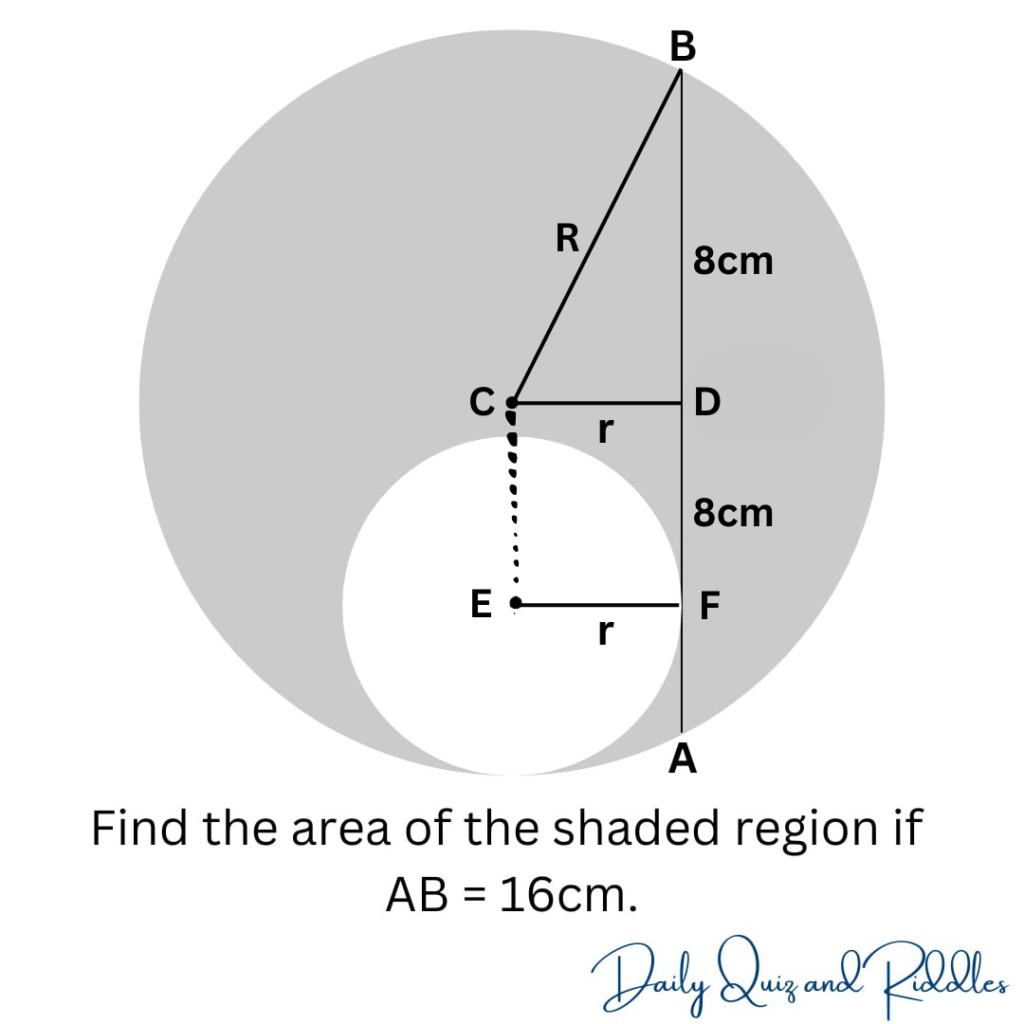
Pythagorean Theorem: We’ll utilize the power of the Pythagorean Theorem to dissect the relationship between the various components of the circles. Consider the triangle BCD, with BD as the hypotenuse and a length of 8cm.
Applying Pythagoras, we have: CB² = BD² + CD²
Now, let’s substitute the known values into the equation: R² – r² = 64
Finding the Shaded Area: Finally, we reach the climax of our quest – calculating the area of the shaded region. We know that the area of a circle is given by πr², where π (pi) is approximately 3.14159.
The area of the shaded portion can be expressed as: Area = πR² – πr² = π(R² – r²) = π(64) = 201.1 square centimeters
Conclusion:
Congratulations on unlocking the mystery of the shaded area! Through the strategic use of Pythagoras and the properties of circles, you navigated through the geometric enigma and emerged victorious.
Remember, mathematical puzzles challenge us to think critically and apply our knowledge in creative ways. The joy of problem-solving lies in the journey of discovery, and with each challenge, we gain deeper insights into the fascinating world of mathematics.