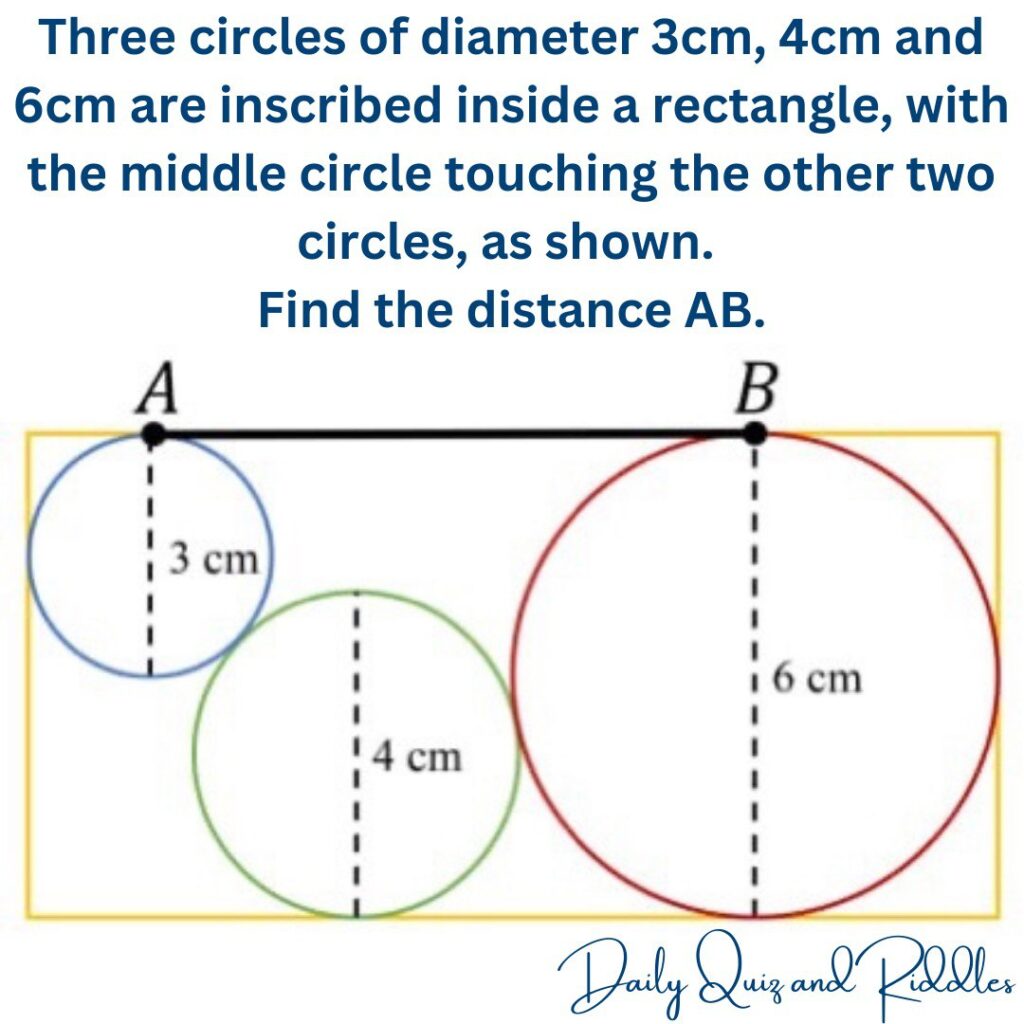
Question:
Three circles of diameter 3cm, 4cm and 6cm are inscribed inside a rectangle, with the middle circle touching the other two circles, as shown. Find the distance AB.
Answer:
7.35 cm
Explanation
Prepare for a geometric challenge that will test your spatial reasoning and problem-solving skills. In this intriguing puzzle, we encounter three circles inscribed inside a rectangle, forming a fascinating configuration. Our quest is to determine the distance AB, a task that requires us to carefully examine the relationships between the circles and their respective dimensions. Get ready to dive into the world of tangency and calculations as we unlock the solution to this captivating problem.
The Puzzle:
Our puzzle begins with three circles of diameters 3cm, 4cm, and 6cm, inscribed inside a rectangle. The middle circle touches the other two circles, forming a unique arrangement. The key to solving this puzzle lies in finding the distance AB, which corresponds to the horizontal distance between the centers of the blue and red circles.
Solution and Calculations: To unravel the puzzle, we break down the problem into manageable steps and employ geometric principles to determine the distances involved.
- Green and Red Circles: First, let’s focus on the green and red circles. By visualizing a right triangle with the horizontal and vertical distances between their centers as its legs as shown below, we can apply the Pythagorean Theorem to find the hypotenuse.
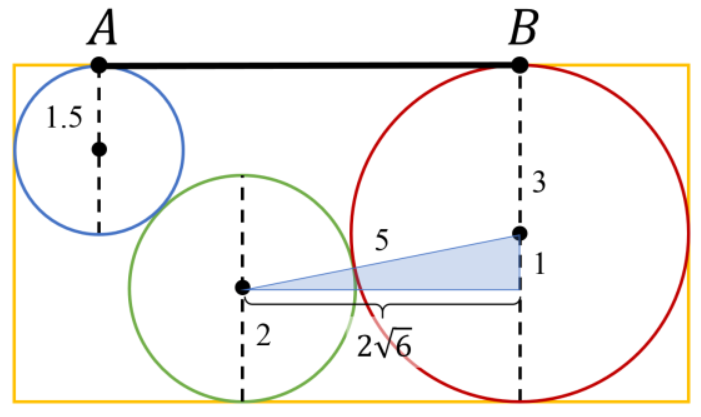
- One leg is the difference of the radii, which is 3cm – 2cm = 1cm.
- The hypotenuse represents the sum of the radii, which is 3cm + 2cm = 5cm.
Applying the Pythagorean Theorem to find the other leg, we calculate √(5^2 – 1^2) = √24 = 2√6.
Therefore, the horizontal distance between the green and red circles is 2√6.
- Blue and Green Circles: Next, let’s examine the relationship between the blue and green circles. Similar to the previous step, we visualize a right triangle with the horizontal and vertical distances between their centers as shown below.
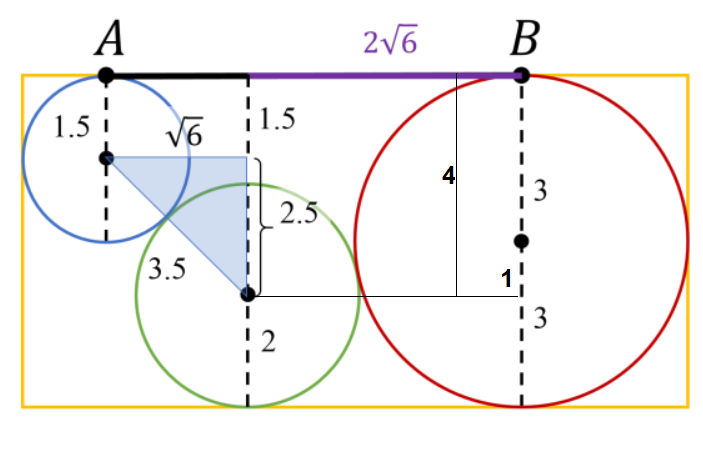
- Knowing that the vertical distance from the middle of the green circle to the top of the square is 4cm and that the distance from the top of the blue circle to its center (radius) is 1.5cm, we can calculate the length of one leg of our triangle to be 4 – 1.5 = 2.5.
- The hypotenuse represents the sum of the radii, which is 1.5cm + 2cm = 3.5cm.
Applying the Pythagorean Theorem to find the other leg, we calculate √(3.5^2 – 2.5^2) = √6.
Therefore, the horizontal distance between the blue and green circles is √6.
- Final Distance AB: Finally, to determine the distance AB, we add the horizontal distances between the green and red circles and between the blue and green circles.
AB = 2√6 + √6 = 3√6 ≈ 7.35 cm.
Conclusion: Congratulations! You successfully deciphered the puzzle and found the distance AB by skillfully applying geometric principles. Through careful calculations and an understanding of tangency, you unlocked the solution and uncovered the hidden relationships within the configuration of circles and the rectangle.
Remember, puzzles like these not only challenge us but also strengthen our analytical thinking and problem-solving abilities. Embrace the joy of geometric puzzles, and continue exploring the fascinating realm of shapes, distances, and intricate configurations.